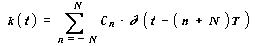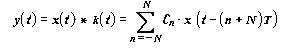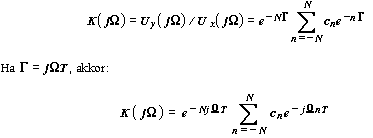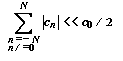A transzverzális szűrő időtartománybeli viselkedését legjobban a Dirac impulzusra
adott válaszából (súlyfüggvény) láthatjuk. Amennyiben a késleltető lánc ideális, azaz a
lánc tagjai veszteségmentesek és frekvenciától függetlenül egyenként
T késleltetésűek, az ideális T-szűrő
kimeneti jele a főjel mindkét oldalán N számú Cn nagyságú impulzusechót
tartalmaz, egymástól T időtartamra (T.3.ábra).
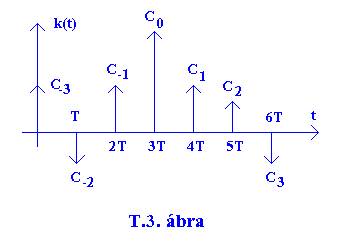
A T-szűrő súlyfüggvénye:
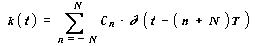
(ahol delta a Dirac függvény jele).
Ha a T-szűrő bemenetére x(t) jel kerül, akkor a kimenetén
megjelenő y(t) jel:
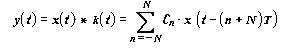
(ahol * a konvolució jele).
A frekvenciatartományba áttérve a T-szűrő átviteli karakterisztikájára irható:
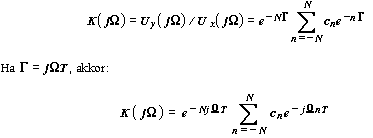
Amennyiben a főjel két oldalán kis echók létehozására van szükség, tehát
feltételezhető, hogy:
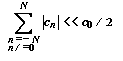 akkor az ideális T-szűrő amplitudó- és futási idő karakterisztikája
közelítően irható:
akkor az ideális T-szűrő amplitudó- és futási idő karakterisztikája
közelítően irható:
 Mint a fenti összefüggésekből kiderül, kis echók esetén az egyes
szimmetrikusan elhelyezkedő leágazások jelei egymástól függetlenül
koszinuszos karakterisztikákat valósitanak meg. Az n-dik koszinuszos
amplitudó- és futási idő karakterisztikakomponens nagyságának
beállitására a együtthatópár áll rendelkezésre, igy a két
karakterisztikakomponens függetlensége is biztositható, tehát az
áramkör általában nem minimálfázisu.
Nyilvánvaló továbbá, hogy az ideális késleltető művonalú T-szűrő
átviteli karakterisztikája 1/T szerint periódikus:
Mint a fenti összefüggésekből kiderül, kis echók esetén az egyes
szimmetrikusan elhelyezkedő leágazások jelei egymástól függetlenül
koszinuszos karakterisztikákat valósitanak meg. Az n-dik koszinuszos
amplitudó- és futási idő karakterisztikakomponens nagyságának
beállitására a együtthatópár áll rendelkezésre, igy a két
karakterisztikakomponens függetlensége is biztositható, tehát az
áramkör általában nem minimálfázisu.
Nyilvánvaló továbbá, hogy az ideális késleltető művonalú T-szűrő
átviteli karakterisztikája 1/T szerint periódikus:
 A megkötés (mintavételi tétel) miatt a T-szűrő karakterisztikájának azonban csak 1/2T
frekvenciáig terjedő sávja választható meg függetlenül.
A megkötés (mintavételi tétel) miatt a T-szűrő karakterisztikájának azonban csak 1/2T
frekvenciáig terjedő sávja választható meg függetlenül.
A T-szűrő kiválóan alkalmazható a 0...1/2T frekvenciasávban csillapítás-
és futási idő korrektorként. A korrekció itt azt jelenti hogy a
T-szűrővel olyan négypólust valósítunk meg, melyet kaszkádba kapcsolunk
a kiegyenlítendő hálózattal, és így az eredő hálózat átviteli
karakterisztikája teljesíti a torzításmentes átvitel kritériumát.