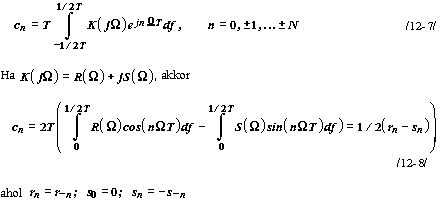
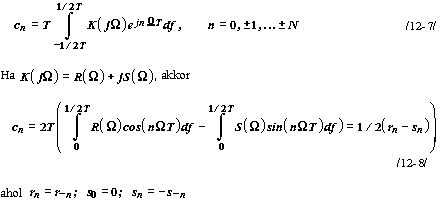
A Fourier-sor módszerrel tehát tulajdonképpen az előirt karakterisztikához tartozó súlyfüggvényt határozzuk meg, majd a megfelelő, a súlyfüggvényt vényt jellemző mintákat választjuk cn -nek. A fenti összefüggés kiértékelése számos speciális esetben /pl. tiszta valós K(jω) lényegesen egyszerűsithető /T.4.ábra/.

Szakadásos függvények /pl. aluláteresztő jellegü K(jω) Fourier-soros approximációja során a gyakorlatilag szükséges sorcsonkitás következtében a szakadások, átmenetek környezetében jelentős berezgéssel kell számolnunk. Hogy ezt az u.n. Gibbs-féle oszcillációt csökkentsük, a szakadások helyén, ill. környezetében a karakterisztikát módositani kell.
Ezt ugy tehetjük meg, hogy a kiválasztott 2N+1 számú súlyfüggvénymintát megszorozzuk egy megfelelő választott wn=w/nT/ u.n. simitó súlyfüggvénnyel. A szorzás a frekvenciatartományban a K(jω) és a keskenysávú W(jω)=F{w(t)} függvények közötti konvoluciónak felel meg.
Viszonylag egyszerű, de igen hatékony simitó függvény a Hamming-féle ablakfüggvény:
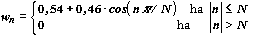
Igy a T-szűrőn beállítandó együtthatók a fenti összefüggés által meghatározott cn értékek és a wk -k szorzataként állnak elő. A simitó függvények alkalmazásával tehát a megvalósitott karakterisztika hullámosságát csökkentjük, de - mint a konvolválásból kitünik - csökken az átmenet meredeksége. /T.4. ábra/